这些天正在试图入门机器学习的相关内容，正好前几天与同学讨论了反向传播算法的一些问题，自己遂花了一些时间来研究了一下，正好也借着这个机会入门一下机器学习的知识，这里记录一下我对于这个算法具体理解和解读。

反向传播算法

定义

反向传播（英语：Backpropagation，缩写为BP）是“误差反向传播”的简称，是一种与最优化方法（如梯度下降法）结合使用的，用来训练人工神经网络的常见方法。该方法对网络中所有权重计算损失函数的梯度。这个梯度会反馈给最优化方法，用来更新权值以最小化损失函数。
反向传播要求有对每个输入值想得到的已知输出，来计算损失函数梯度。因此，它通常被认为是一种监督式学习方法，虽然它也用在一些无监督网络（如自动编码器）中。它是多层前馈网络的Delta规则的推广，可以用链式法则对每层迭代计算梯度。反向传播要求人工神经元（或“节点”）的激励函数可微。

——来自Wiki百科的定义

Cost Function(代价函数)

代价函数（有的地方也叫损失函数，Loss Function）在机器学习中的每一种算法中都很重要，因为训练模型的过程就是优化代价函数的过程，代价函数对每个参数的偏导数就是梯度下降中提到的梯度，防止过拟合时添加的正则化项也是加在代价函数后面的。
代价函数非常好理解，我觉得其实就是，反映神经网络输出的结果与训练样本的y之间的差别的函数（其中输入变量是神经网络的权重参数）。这个函数要具有一些特性，一般情况下，我们要尽可能的最小化代价函数，寻找代价函数的全局最小值，从而找到神经网络的最优权值参数，这里不展开讨论，仅仅解释一下概念。

明确我们的目标

在完成一次前向传播后，已知$J(\Theta)$也就是$C(\Theta)$（代价函数），为了实现梯度下降：$\theta^{(l)}:=\theta^{(l)}-\frac{\partial C}{\partial \theta^{(l)}}$。我们需要求$\frac{\partial C}{\partial \theta^{(l)}}$。

算法流程详解

-注：此处以吴恩达机器学习视频中讲解的算法首先进行阐述。
假设目前我们已经有了一个多层，但是网络权值参数还没有更新。

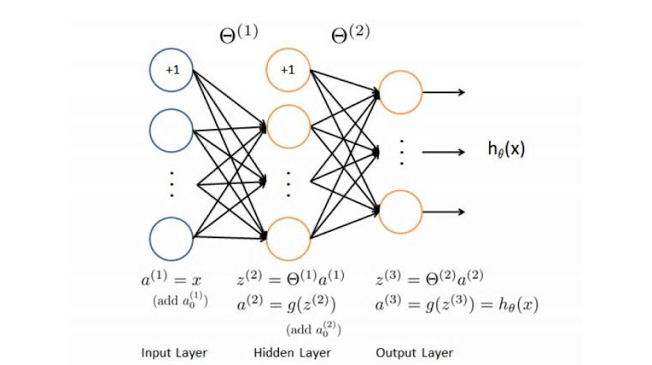
首先，我要说明一下计算中所用到的参数符号及其解释：

• $x_j$仅仅表示最左侧输入层的输入，下标$j$表示第$j$个单元(unit)。

• $\theta_{i,j}^{(l)}$表示从第$(l)$层的第$i$个单元到第$(l+1)$层的第j个单元的$\theta$

• $\theta^{(l)}$是$\theta_{i,j}^{(l)}$的矩阵形式。$\theta^{(l)}$中的每一行（$i$相同）是$a_i^{(l)}$所散发给下一层的参数，是$a_j^{(l)}$的接收参数

• $l$表示网络的总层数，$l=$网络总层数

• $a_{j}^{(l)}$表示表示第$l$层的第$j$个神经元的输出

• $z_{j}^{(l)}$表示表示第$l$层的第$j$个神经元的输入

• $a_{j}^{(l)}=g^{\prime}\left(z_{j}^{(l)}\right)=\operatorname{sigmoid}^{\prime}\left(z_{j}^{(l)}\right)$其中sigmoid是激活函数

• $a_{j}^{(l-1)}$和$z_{j}^{(l)}$的转化如图所示

• $C(\Theta)$是代价函数，在这里
  $$J(\Theta)=C(\Theta)=\-\frac{1}{m} \sum_{i=1}^{m}
  \sum_{k=1}^{k}\left[y_{k}^{(i)} \log \left(\left(h_{\Theta}\left(x^{(i)}\right)\right){k}\right)+\left(1-y{k}^{(i)}\right) \log \left(1-\left(h_{\Theta}\left(x^{(i)}\right)\right){k}\right)\right]\+\frac{\lambda}{2 m} \sum{l=1}^{L-1}
  \sum_{i=1}^{s l} \sum_{j=1}^{s_{(l+1)}}\left(\Theta_{j, i}^{(l)}\right)^{2}$$

• $s_{(l)}$表示$a^{(l)}$神经元的个数

• 当然你也可以使用其他的代价函数，还有一个常用的代价函数是二次代价函数：

  $$C=\frac{1}{2 n} \sum_{x}\left|y(x)-a^{L}(x)\right|^{2}$$

下面放一张吴恩达机器学习反向传播的算法的图片：

下面我将一行一行进行讲解：

1. 首先第一行没什么说的，就是目前有m个训练样本，接下来我们要对这m个训练样本进行一些神奇的操作，使得构建的神经网络更加准确。

2. 第二行设置了一个变量，每一个$\triangle_{i j}^{(l)}$都对应着$\theta_{i, j}^{(l)}$，这里$\triangle_{i j}^{(l)}$只是用来计算$\frac{\partial}{\partial \Theta_{i j}^{(l)}} J(\Theta)$的一个变量，后面我会详细进行解释。

3. 第三行是一个循环语句，对于每一对训练数据$\left(x^{(i)}, y^{(i)}\right)$(一共m个),都进行如下的操作。

4. 首先将训练数据的x输入，也就是$a^{(1)}=x^{(i)}$。

5. 首先进行正向传播（假设$\theta_{i,j}^{(l)}$都有初值，这里的初值后面还会通过反向传播进行更新，应该是可以人为随意确定），这里过程就忽略了，总之通过正向传播我可得到每一层的$a^{(l)}$和$z_{j}^{(l)}$（当$l=2,3, \ldots, L$的时候）

6. 下面开始反向传播的过程，首先计算一个值$\delta^{(L)}$，我们通常把这个值叫做”误差”，每一个神经元以及每一对训练数据都会对应一个误差值，关于这个误差值为什么这么计算，以及如何用最后一层的误差值来计算前面几层的误差值（其实就是所谓的反向传播），我会放在后文来解释。总之这个目前我们可以理解为，$\delta$用来表示与神经元计算结果与正确结果的偏差值，由于计算结果（最后一层）存在”误差”，所以将最后一层的”误差”通过一定的计算方法来反推各个神经元的”误差”，然后利用每个神经元的每个训练样本所找到的误差之和来更新$\theta_{i, j}^{(l)}$，这就是我们反向传播的基本目标，后面我会详细讲解这之中的公式。最后一层”误差”的计算公式是这样的：$\delta^{(L)}=a^{(L)}-y$。
   其中L表示最后一层（输出层），这个公式看起来比较合理，你可能会想为什么要这么计算，请 不要着急，关于为什么这么计算，它是有一定的道理的，我会放在后面进行解释。

7. 下面将进行与正向传播相似的过程，计算$\delta^{(L-1)}, \delta^{(L-2)}, \ldots, \delta^{(2)}$，(计算这些参数的算法我将在后文进行具体的阐述)，当然第一层就是输入层，也不存在所谓的”误差”，所以并不需要考虑$\delta^{(1)}$
   然后将每个训练样本计算出来的误差先乘以$a_{j}^{(l)}$再进行累加，这个大概的意思是将每个训练样本存在的误差都综合起来，后文我会详细阐述为什么要这么做。

8. 我们进行最后一步操作（关于为什么要这么做，我会在后面进行详细的解释。）：
   $$
   \begin{aligned}
   &\cdot D_{i, j}^{(l)}:=\frac{1}{m}\left(\Delta_{i, j}^{(l)}+\lambda \Theta_{i, j}^{(l)}\right), i f j \neq 0\
   &\cdot D_{i, j}^{(l)}:=\frac{1}{m} \Delta_{i, j}^{(l)}, i f j=0
   \end{aligned}
   $$

通过上一步的式子，我们可以计算出我们的梯度目标：
$$
\frac{\partial}{\partial \Theta_{i j}^{(l)}} J(\Theta)=D_{i j}^{(l)}
$$
关于为什么要这么算，我会在后面讲解。

关于$\delta$

$\delta$在很多书中翻译为‘误差’，但这与模型预测值与样本y之间的误差不是一个概念。实际上$\delta$是一个微分值。书上将其定义为：
$$
\delta(l)=\frac{\partial C}{\partial z^{(l)}}
$$
我觉得它这么定义是为了简化我们的计算，当然如果没有$\delta$，我们也完全可以使用链式法则的方法来一一计算$\theta^{(l)}$，有了这个中间值，可以简化计算，不用对每一层θ的偏导计算都从网络的输出层开始重新计算一遍。事实上没有这个中间值你也能完整表达整个网络的梯度求导，只不过网络层数一多进行计算的式子会非常复杂(容易晕，亲身体会)。
我们的别忘了我们的目的是求$\frac{\partial C}{\partial \theta^{(l)}}$，如果我们知道$\delta(l)=\frac{\partial C}{\partial z^{(l)}}$，那么由链式法则我们可以知道
$$
\frac{\partial C}{\partial \theta^{(l)}}=\frac{\partial C}{\partial z^{(l+1)}} \cdot \frac{\partial z^{(l+1)}}{\partial \theta^{(l)}}=\delta^{(l+1)} \cdot \frac{\partial z^{(l+1)}}{\partial \theta^{(l)}}
$$
而$\frac{\partial z^{(l+1)}}{\partial \theta^{(l)}}$恰好等于$a^{(l)}$（线性函数求导）。
因此：
$$
\frac{\partial C}{\partial \theta^{(l)}}=\delta^{(l+1)} \cdot a^{(l)}
$$
有了以上的式子，如果我们找到$\theta^{(l)}$和$\theta^{(l+1)}$之间的关系，那我们就可以计算出所有权重的梯度啦！

寻找层与层之间”误差”的关系

首先我们已知：
$$
z^{(l+1)}=\theta^{(l)} \cdot \text { sigmoid }\left(z^{(l)}\right)
$$

$$
\text {sigmoid}^{\prime}\left(z^{(l)}\right)=a^{(l)} \cdot\left(1-a^{(l)}\right)
$$
那么由链式法则我们可以知道：
$$
\delta^{(l)}=\frac{\partial C}{\partial z^{(l)}}=\frac{\partial C}{\partial z^{(l+1)}} \cdot \frac{\partial z^{(l+1)}}{\partial z^{(l)}}=\\delta^{(l+1)} \cdot\left(\theta^{(l)}\right)^{T} \cdot a^{(l)} \cdot\left(1-a^{(l)}\right)
$$
大功告成！我们找到了层与层之间误差的关系，同时这也是吴恩达视频里面提到的公式：

确定输出层的”误差”

由以上的定义我们可以知道，$\delta(l)=\frac{\partial C}{\partial z^{(l)}}$，这里将解释输出层的”误差”为什么是$\delta^{(L)}=a^{(L)}-y$。
我们知道$\delta^{(l)}$与$\delta^{(l+1)}$之间的关系，就能从输出层一层层的往输入层推。但是在输出层因为没有下一层节点，所以$\delta^{(l)}$需要用另一种方式确定。
根据定义：
$$ \delta(l)=\frac{\partial C}{\partial z^{(l)}} $$
由前文中我们可以知道代价函数为：

$$J(\Theta)=C(\Theta)=\-\frac{1}{m} \sum_{i=1}^{m}
\sum_{k=1}^{k}\left[y_{k}^{(i)} \log \left(\left(h_{\Theta}\left(x^{(i)}\right)\right){k}\right)+\left(1-y{k}^{(i)}\right) \log \left(1-\left(h_{\Theta}\left(x^{(i)}\right)\right){k}\right)\right]\+\frac{\lambda}{2 m} \sum{l=1}^{L-1}
\sum_{i=1}^{s l} \sum_{j=1}^{s_{(l+1)}}\left(\Theta_{j, i}^{(l)}\right)^{2}$$

我们考虑单个训练样本，省略m，并且认为输出神经元只有一个，那么式子可以简化为：
$$J(\theta)=C(\theta)=-\left[y \cdot \log \left(a^{(L)}\right)+(1-y) \log \left(1-a^{(L)}\right)\right]$$
我们接着推导：
$$\frac{\partial C}{\partial z^{(L)}}=\frac{\partial J(\Theta)}{\partial a^{(L)}} \cdot \frac{\partial a^{(L)}}{\partial z^{(L)}}$$
$$\frac{\partial C}{\partial a^{(L)}}=\frac{a^{(L)}-y}{\left(1-a^{(L)}\right) \cdot a^{(L)}}$$
$$\frac{\partial a^{(L)}}{\partial z^{(L)}}=a^{(L)} \cdot\left(1-a^{(L)}\right)$$
因此：
$$\frac{\partial C}{\partial z^{(L)}}=\delta^{(L)}=a^{(L)}-y$$
大功告成！这个结果似乎出乎意料，这正好与我们概念上理解的误差如此相似！我想这大概就是数学之美吧~

笔者补充

关于$\Delta_{i, j}^{(l)}:=\Delta_{i, j}^{(l)}+a_{j}^{(l)} \delta_{i}^{(l+1)}$这个式子：
上面已经推导过了，
$$\frac{\partial C}{\partial \theta^{(l)}}=\delta^{(l+1)} \cdot a^{(l)}$$
根据以上式子，我们可以了解到$\Delta$是用来将每一个样本计算出来的梯度值进行累加，因为我们刚才是将m的条数看作为1，而实际上有很多训练数据，这个操作可以看作是原代价函数的中的m个累加操作，而下面这个式子：
$$\begin{aligned}
&\cdot D_{i, j}^{(l)}:=\frac{1}{m}\left(\Delta_{i, j}^{(l)}+\lambda \Theta_{i, j}^{(l)}\right), i f j \neq 0\
&\cdot D_{i, j}^{(l)}:=\frac{1}{m} \Delta_{i, j}^{(l)}, i f j=0
\end{aligned}
$$
这两个式子是由原来那个十分复杂的代价函数来求梯度所得到的。其中j=0时是表示偏移项b的梯度，j不等于0时是表示一般项的梯度（其中$\lambda \Theta_{i, j}^{(l)}$应该表示的是正则项）。
有了梯度值，我们设定了合理的梯度下降参数，就可以更新神经网络的权值啦！


此外，如果你觉得$\delta$这个概念理解起来太困难，也完全没有关系，我认为可以完全不需要理解$\delta$这个概念，直接利用链式法则，从最后一层层层向前推导，其实答案是一样，原理都相同。而且我看了网上这么多的教程，网上对$\delta$这个概念的定义很乱。使用不同的cost function，按照原来的定义来计算$\delta$，最后一层的值就不再是本文中的式子了（这也打破了直观上的”误差”似乎是一种巧合，或者前人专门定义成这样，方便计算与理解）。我们还是不要太纠结于对$\delta$的定义，当然本文使用的是吴恩达的定义，我觉得它的更具权威性，也好理解。
我也是菜鸟一枚，希望写的不对的地方，还希望大家多多指正。

参考

1.吴恩达机器学习视频-B站-反向传播算法
2.https://blog.csdn.net/u014313009/article/details/51039334
3.https://blog.csdn.net/zhq9695/article/details/82864551

另外吹一波公式识别软件(OCR)，Mathpix实在是太强大啦！图片，手写公式都能完美转化为Latex格式，简直是科研人的福音，只可惜现在收费了，一个月的免费次数只有50次，嘤嘤嘤，太可惜了。