Numpy中的向量

本文总结了关于Numpy向量使用的一些问题，包括向量与矩阵，Python 中的广播（Broadcasting in Python）的使用与原理。

向量与矩阵

首先介绍一下Numpy中数组的概念，这个东西容易与矩阵混淆，首先设置$a=np.random.randn(5)$，这样会生成存储在数组 $a$ 中的5个高斯随机数变量。之后输出 $a$，从屏幕上可以得知，此时 $a$ 的shape（形状）是一个$(5,)$的结构。这在Python中被称作一个一维数组。它既不是一个行向量也不是一个列向量，这也导致它有一些不是很直观的效果。举个例子，如果我输出一个转置阵，最终结果它会和$a$看起来一样，所以$a$和$a$的转置阵最终结果看起来一样。而如果我输出$a$和$a$的转置阵的内积，你可能会想：$a$乘以$a$的转置返回给你的可能会是一个矩阵。但是如果我这样做，你只会得到一个数。

import numpy as np #导入numpy库
a=np.random.randn(5)
print(a)
print(a.shape)
print(a.T)
print(np.dot(a,a.T))

结果

[ 1.38747875  1.05981906 -0.41137174  0.85581765  0.25313936]
(5,)
[ 1.38747875  1.05981906 -0.41137174  0.85581765  0.25313936]
4.014043815271083

所以编写神经网络时，不要使用shape为 (5,)、(n,) 或者其他一维数组的数据结构。相反，如果设置 $a$ 为$(5,1)$，那么这就将置于5行1列向量中。在先前的操作里 $a$ 和 $a$ 的转置看起来一样，而现在这样的 $a$ 变成一个新的 $a$ 的转置，并且它是一个行向量。请注意一个细微的差别，在这种数据结构中，当我们输出 $a$ 的转置时有两对方括号，而之前只有一对方括号，所以这就是1行5列的矩阵和一维数组的差别。

import numpy as np #导入numpy库
a=np.random.randn(5,1)
print(a)
print(a.shape)
print(a.T)
print(np.dot(a,a.T))

结果

 [ 0.14745407]
 [ 0.04916029]
 [-0.78656516]
 [ 1.37759773]]
(5, 1)
[[-0.28745951  0.14745407  0.04916029 -0.78656516  1.37759773]]
[[ 0.08263297 -0.04238707 -0.01413159  0.22610564 -0.39600357]
 [-0.04238707  0.0217427   0.00724889 -0.11598223  0.20313239]
 [-0.01413159  0.00724889  0.00241673 -0.03866777  0.06772311]
 [ 0.22610564 -0.11598223 -0.03866777  0.61868476 -1.08357039]
 [-0.39600357  0.20313239  0.06772311 -1.08357039  1.89777551]]

就我们刚才看到的，再进一步说明。首先我们刚刚运行的命令是这个 $(a=np.random.randn(5))$，它生成了一个数据结构$a$，其中$a.shape$是$(5,)$。这被称作 $a$ 的一维数组，同时这也是一个非常有趣的数据结构。它不像行向量和列向量那样表现的很一致，这使得它带来一些不直观的影响。所以我觉得，当在编程练习或者在执行逻辑回归和神经网络时，最好不使用这些一维数组。

最好不要这样写：

from numpy import *

# 数组
v1 = array([1, 0, 1])
v11 = array([1, 1, 1])

# 2*3矩阵
v2 = array([[1, 1, 2], [1, 1, 0]])

# 线性代数矩阵乘法，行乘列，再相加
print("一维向量dot： ", dot(v11, v1))
print("一维dot二维： ", dot(v2, v1))

我们来看看结果：

一维向量dot：  2
一维dot二维：  [3 1]

第一个似乎很正确，数组的内积，事实上dot函数如果传入两个数组的话，它会计算出数组的内积，即对应相乘，第二个似乎不符合常理，如果是一个2x3的矩阵乘以1x3的矩阵，那么是如何都说不通的，其实dot帮v1进行了reshape操作(reshape顾名思义，就是帮助数组或者矩阵进行行列的调整，具体作用可以百度之)，而且这种写法了混淆了一维数组和矩阵，直接拿矩阵与一维数组相乘，实际上python里面是对v1进行了reshape操作，reshape后，v1变成了[[1]，[0]，[1]]，这样的乘法就符合规则了。

广播（Broadcasting in Python）

简单来说，broadcasting可以这样理解：如果你有一个$m \times n$的矩阵，让它加减乘除一个 $1 \times n$的矩阵，它会被复制m次，成为一个$m \times n$的矩阵，然后再逐元素地进行加减乘除操作。同样地对$m \times 1$的矩阵成立。

下面这条规则十分重要：n

如果两个数组的后缘维度的轴长度相符或其中一方的轴长度为1，则认为它们是广播兼容的。广播会在缺失维度和轴长度为1的维度上进行。

A = np.array([1,2,3])
result = A + 100
print(result)

输出为

[101 102 103]

不需要写A + [100, 100, 100]。

A = np.array([[1,2,3,5],[1,2,3,5],[1,2,3,5]])
cal = np.array([100,1,1,1])
result = A/cal
print(result)

输出为：

[[0.01 2.   3.   5.  ]
 [0.01 2.   3.   5.  ]
 [0.01 2.   3.   5.  ]]

这条指令将 $3\times 4$的矩阵$A$除以一个$1 \times 4$的矩阵，得到了一个 $3 \times 4$的结果矩阵,上面其实等价于：

A = np.array([[1,2,3,5],[1,2,3,5],[1,2,3,5]])
cal = np.array([100,1,1,1])
result = A/cal.reshape(1,4)
print(result)

也就是说，python会自动帮它执行reshape操作。

A/cal.reshape(1,4)指令则调用了numpy中的广播机制。这里使用 $3 \times 4$的矩阵$A$除以 $1 \times 4$的矩阵$cal$。技术上来讲，其实并不需要再将矩阵$cal$ reshape(重塑)成 $1 \times 4$，因为矩阵$cal$本身已经是 $1 \times 4$了。但是当我们写代码时不确定矩阵维度的时候，通常会对矩阵进行重塑来确保得到我们想要的列向量或行向量。重塑操作reshape是一个常量时间的操作，时间复杂度是$O(1)$，它的调用代价极低。

就像我们刚才说的：

如果两个数组的后缘维度的轴长度相符或其中一方的轴长度为1，则认为它们是广播兼容的。广播会在缺失维度和轴长度为1的维度上进行。

上面的例子就是矩阵 $A_{3,4}$ 后缘维度的轴长度是4，而矩阵 $cal_{1,4}$ 的后缘维度也是4，则他们满足后缘维度轴长度相符，可以进行广播。广播会在轴长度为1的维度进行，轴长度为1的维度对应axis=0，即垂直方向，矩阵 $$\text{cal}{1,4}$$ 沿axis=0(垂直方向)复制成为 $\text{cal_temp}{3,4}$ ，之后两者进行逐元素除法运算。

总结一下：

矩阵 $A_{m,n}$ 和矩阵 $B_{1,n}$ 进行四则运算，后缘维度轴长度相符，可以广播，广播沿着轴长度为1的轴进行，即 $B_{1,n}$ 广播成为 ${B_{m,n}}’$ ，之后做逐元素四则运算。

矩阵 $A_{m,n}$ 和矩阵 $B_{m,1}$ 进行四则运算，后缘维度轴长度不相符，但其中一方轴长度为1，可以广播，广播沿着轴长度为1的轴进行，即 $B_{m,1}$ 广播成为 ${B_{m,n}}’$ ，之后做逐元素四则运算。

矩阵 $A_{m,1}$ 和常数$ R$ 进行四则运算，后缘维度轴长度不相符，但其中一方轴长度为1，可以广播，广播沿着缺失维度和轴长度为1的轴进行，缺失维度就是axis=0,轴长度为1的轴是axis=1，即$R$广播成为 ${B_{m,1}}’$ ，之后做逐元素四则运算。

如下图所示：

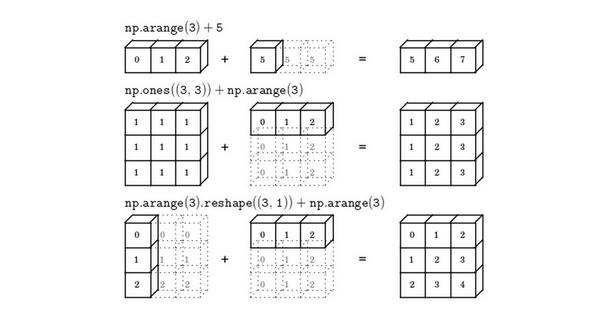
反正不是$m \times n$和$ 1 \times n$，那就是$m \times n$和$ m \times 1$只有这两种情况是可行的

如果是$m \times n$和$n \times 1$或者$m \times n$和$ 1 \times m$这两种都是不行的